

Resumen
En el presente trabajo se muestra los resultados obtenidos al aplicar la escala de atribución de la motivación al logro, al implementar la calculadora TI- Nspire CX CAS como herramienta tecnológica en alumnos de la carrera de Ingeniería Química Petrolera. El trabajo estuvo guiado por la didáctica de la Matemática en Contexto de las Ciencias. Se analizaron 22 ítems de la escala atribucional de motivación al logro antes y después de implementada la tecnología Texas Instrument en 29 alumnos de tercer semestre de la carrera de Ingeniería Química Petrolera. Los resultados estadísticos muestran predominantemente un cambio de atribuciones respecto al logro de justicia en la evaluación hacia las ganas de estudiar, de igual manera se observa un cambio en las causas atribucionales percibidas por los alumnos ante los exámenes y la suerte, hacia las atribuciones del interés y esfuerzo del alumno y la capacidad pedagógica del docente.
Palabras clave: Escala atribucional, motivación al logro, tecnología.
Introducción
Desde finales del siglo pasado, diferentes especialistas del área de las ciencias sociales han dedicado sus estudios al tema de la incorporación de las tecnologías de la información y la comunicación (TIC) en la educación superior. Organismos internacionales, como la UNESCO, han enfatizado sobre la necesidad de cambiar el paradigma de formación de este nivel educativo con el propósito de adecuarlo a las exigencias internas de los países, del fenómeno de la globalización, de la sociedad del conocimiento y el desarrollo científico-tecnológico.
Esto hace renacer interrogantes sobre la importancia e influencia de factores como la motivación al logro y el conocimiento previo sobre el aprendizaje y el rendimiento de los estudiantes, en tanto que las modalidades alternativas incluyen innovaciones en los métodos, las estrategias y las técnicas instruccionales, así como en el diseño de los materiales didácticos en función de alcanzar los objetivos de aprendizaje y formar las respectivas competencias en el profesional egresado de la universidad.
La motivación al logro consiste en una red de conexiones cognitivo-afectivas relacionadas con el desarrollo personal e impulsa a las personas a exigirse más, a rendir más, a usar eficientemente las capacidades, las destrezas y los conocimientos adquiridos. Entonces, cuando se han establecido metas, tareas, creencias y actividades facilitadoras de logro, la acción o desempeño del estudiante aprendiz es un acto consciente con intencionalidad. Por ello, se supone que el efecto de la motivación al logro se refleja en la elaboración de aquellas tareas que representan conflictos cognitivos generadores de nuevo conocimiento.
Existe un acuerdo entre teóricos e investigadores (Carrasco, 1993; Comisión Nacional para Definir el Perfil de Entrada del Estudiante Universitario, 2003; Good y Brophy, 1996; Pérez y Romero, 1992), en decir que la motivación es un factor interno de efecto catalítico que origina, mantiene y orienta la conducta hacia metas específicas, que es importante en el aprendizaje de estudiantes universitarios. Es decir, la motivación mueve, imprime orientación y energiza a los deseos e intenciones del estudiante hasta el punto de hacerlo actuar en la dirección de logro y realización. Dicho efecto, según Ausubel, Novak y Hanesian (1983), debido a la persistencia, se refleja en el rendimiento académico y existe la tendencia a pensar que las razones intrínsecas son más determinantes que las extrínsecas.
Por otro lado, algunos estudios demuestran que el alumno que utiliza tecnología en su proceso de enseñanza aprendizaje tiene más tiempo para explorar, descubrir, entender y aplicar conceptos y llegar a la resolución de problemas, elevando así el nivel de pensamiento del estudiante. (Martínez C., 1996; Ramírez B., 1996; De Faria, E. 2000). El National Council of Teachers of Mathematics desde octubre de 1996 recomienda la incorporación de la calculadora en todos los niveles de la enseñanza de matemática para: explorar y experimentar nuevas formas de enseñar con ideas matemáticas tales como patrones, propiedades numéricas y algebraicas, y funciones, así como el construir modelos, resolver problemas con datos reales y elevar el nivel de abstracción y generalización.
Para que el estudiante pueda vivir nuevas experiencias matemáticas (difíciles de lograr en medios tradicionales como el lápiz y el papel) en las que se pueda manipular directamente los objetos matemáticos dentro de un ambiente de exploración, Gómez (1997) considera que es indispensable utilizar la tecnología para abrir espacios. Esto es posible ya que se puede manejar dinámicamente los objetos matemáticos en múltiples sistemas de representación dentro de esquemas interactivos, lo que es fundamental para el aprendizaje de los estudiantes.
Un punto importante de consideración al incorporar tecnología se refleja en la decisión de las metodologías o teorías de aprendizaje a utilizar en el proceso educativo, de manera que estas permitan a los estudiantes construir sus conocimientos, asumir la responsabilidad de su aprendizaje y el desarrollo del pensamiento crítico y creativo, porque la tecnología no es un fin en sí mismo sino un medio.
A través de esta investigación presentamos por una lado, la metodología de trabajo para implementar nueva tecnología a la enseñanza de las ecuaciones diferenciales al utilizar como herramienta tecnológica de apoyo la calculadora TI – Nspire CX CAS, por el otro presentamos los resultados estadísticos del estudio para la prueba de Student de dos medias de los rendimientos académicos obtenidos en los grupo control y testigo.
Objetivo
Estudiar el efecto que la implementación de la tecnología en estudiantes del tercer semestre de educación superior del Instituto Politécnico Nacional (IPN) tiene sobre la motivación al logro a través de la escala atribucional de la motivación.
Marco teórico
El trabajo se fundamenta en la teoría de la Matemática en el Contexto de las Ciencias, la cual reflexiona acerca de la vinculación que debe existir entre la matemática y las ciencias, la articulación entre la matemática y la vida cotidiana, así como la relación entre la matemática con las actividades laborales y profesionales.
La etapa de la didáctica de la Matemática en Contexto de las Ciencias es precisamente en la que se puede observar indicadores más tangibles para su seguimiento, en términos de conocimientos, habilidades, aptitudes, destrezas, valores y actitudes, con la finalidad de saber trabajar en equipo, tener conocimiento amplio de las TIC como herramientas de trabajo, reconocer y manipular objeto de estudio; estar capacitado para enfrentar y resolver cualquier problema del área profesional académicamente hablando, a pesar de que no se contempla el uso de calculadoras, ni software matemáticos o paquetes diseñados por los propios profesores (Camarena, 2001).
Tecnología utilizada
Como herramienta de apoyo para este trabajo se utilizó la calculadora Texas TI- Nspire CX CAS que permite manipular múltiples representaciones, además de contar con un avanzado sistema de cálculo simbólico (CAS). Con esta, es posible articular representaciones gráficas, representaciones geométricas, representaciones tabulares, representación de datos numéricos en gráficas y tablas, con opción a ajuste de curvas con métodos de regresión, realizar operaciones matriciales, maneja números complejos, así como la simulación en tiempo real de procesos químicos, físicos y termodinámicos a través del uso de los sensores de temperatura, movimiento, concentración, presión, pH, intensidad luminosa, intensidad de corriente y más brindándole un lugar muy exclusivo como tecnología de punta en el aula y el laboratorio. En la figura 1 se observa por separado la representación analítica y gráfica de una función compuesta entre una recta con pendiente positiva a 45 grados y una parábola que abre hacia el lado izquierdo que muestra un editor de ecuaciones y un graficador.

La misma función se aprecia conjuntamente en la pantalla de la calculadora TI – Nspire CX CAS (figura 2), con la ventaja de identificar, registrar y manipular analíticamente los principales puntos del análisis de la función, mejorando el proceso de visualización de estas representaciones para el alumno.

Figura 2. Representación gráfica y analítica de una función en la calculadora TI –Nspire CX CAS
Esta tecnología adicionalmente permite navegar entre hasta 30 calculadoras simultáneamente en el aula a través del sistema Navigator con lo que el proceso de aprendizaje de los alumnos es dosificado de mejor forma dando inclusive a cada alumno atención personalizada. La figura 3 muestra un grupo de alumnos trabajando simultáneamente con aplicaciones a funciones en el sistema Navigator.

Figura 3. Alumnos trabajando con el sistema Navigator
Metodología
El trabajo de investigación consistió en una intervención metodológica basada en la didáctica de la Matemática en Contexto de las Ciencia, donde se condujo la intervención en tres etapas.
La muestra estuvo conformada por el grupo control con 29 alumnos estudiantes de ingeniería química de la ESIQIE que cursaron la asignatura de ecuaciones diferenciales aplicadas.
En la etapa uno llamada “andamiaje” el grupo manipuló en un primer acercamiento la calculadora TI- Nspire CX CAS de tal manera que pudiesen realizar cálculos analíticos y la graficación correspondiente de los conceptos estudiados, como se observa en la figura 4.

Figura 4. Representación gráfica en la calculadora TI –Nspire CX CAS
Cabe aclarar que cada uno de los alumnos contó con una calculadora para su uso personal la cual le fue facilitada cada una de las sesiones de clase. Lo anterior fue posible ya que la ESIQIE cuenta con un soporte tecnológico de más de 90 calculadoras en sus tres departamentos para uso del alumnado.
Posteriormente en la segunda etapa, una secuencia didáctica para la asignatura de ecuaciones diferenciales aplicadas se presentó al grupo control con actividades complementarias a manera de repaso y retroalimentación para lograr la visualización de conceptos matemáticos en diferentes representaciones semióticas. El propósito fue fomentar el atractivo intrínseco de las tareas de aprendizaje y lograr que éste fuese significativo. Se buscó activar la curiosidad y el interés del alumno en el contenido del tema a tratar, al utilizar las herramientas aprendidas en la calculadora y visualizar diferentes formas del concepto. Se presentó la información nueva en forma poco rutinaria a través de representaciones gráficas principalmente. En esta etapa se observó una reducción de tiempo de ejecución por un mayor tiempo de reflexión por parte del alumno.
Adicionalmente se realizó programación básica con la calculadora, para crear programas de resolución de la aplicación de las ecuaciones diferenciales a mezclas y enfriamiento de Newton. La figura 5 muestra la imagen de una aplicación de la calculadora TI- Nspire CAS a la resolución de las ecuaciones diferenciales utilizando el software de la misma, pudiéndose instalar éste tanto en un ordenador como una lapto para trabajar fácilmente en aplicaciones de 
 Windows.
Windows.
Figura 5. Utilización del software de programación dela calculadora TI- Nspire CX CAS para resolver problemas de mezclas.
Finalmente en la última etapa se realizaron demostraciones en tiempo real de las aplicaciones a las ecuaciones diferenciales a través del uso de los sensores (en este caso de temperatura, intensidad luminosa y pH), lo que permitió observar los fenómenos estudiados en clase. La metodología concluyó con el proyecto el “1° Concurso aplicación de las ecuaciones diferenciales con herramientas computacionales”. De esta manera, en el aula el alumno pudo apreciar un calentamiento y enfriamiento de una sustancia para ejemplificar la Ley de enfriamiento de Newton, las curvas de saturación de soluciones como ejemplo de mezclas y la disminución de la intensidad de luz de una fuente luminosa a través de un tubo, Ver figura 6.


Figura 6.Experimentación de alcalinidad de una mezcla y registro de intensidad luminosa
Diversas posiciones teóricas e investigaciones recientes subrayan la importancia de tomar en cuenta los factores motivacionales que inciden en el aprendizaje, para Weiner (1985), el tipo de atribuciones que realice el estudiante determinará tanto las expectativas como las metas, las cuales podrán considerarse como facilitadoras u obstaculizadoras del futuro éxito académico.
Este estudio tiene como objetivo analizar las propiedades psicométricas de la Escala Atribucional de Motivación de Logro (EMAL) en 29 alumnos. Se midieron las atribuciones de la escala atribucional de motivación de logro EAML al aplicar el instrumento A1 conformado por 22 reactivos de diferencial semántico, distribuidos en las siguientes dimensiones: motivación de interés (5 reactivos), motivación de tarea/ capacidad (5 reactivos), motivación de esfuerzo (5 reactivos), motivación de exámenes (5 reactivos) y motivación de competencia del profesor (2 reactivos). Los resultados se valoran sobre una escala Likert de 1 a 9 puntos. Los reactivos del EMAL-G están redactados para evaluar las expectativas de éxito o fracaso en la asignatura de ecuaciones diferenciales contextualizadas (EDCA), ver anexo A1.
Análisis de resultados
Durante el proceso de implementación de la didáctica de la Matemática en Contexto se aplicó el instrumento A1, y se pudo apreciar que los alumnos atribuyeron el logro del éxito académico a la capacidad pedagógica del profesor con una media de 8.8 y en segunda instancia a la justicia de la nota obtenida que recibían 8.37.
En este momento durante la intervención didáctica, los alumnos estaban motivados más extrínsecamente por la capacidad pedagógica del docente que por la misma estrategia didáctica de la Matemática en Contexto, ver tabla 1.1. Situación que cambió completamente después de volver a aplicar el instrumento E1 al término de la implementación de la estrategia didáctica, ya que los alumnos cambiaron su visión de la atribución del logro del éxito hacia una motivación intrínseca como se aprecia en la tabla 1.2; donde las medias de los ítems más altos se relacionan a la motivación por el interés por estudiar (8.8), el afán (8.4) y las ganas (8.63) por aprender.
La mayoría de los alumnos no atribuye valores altos a los ítems relacionados con la subjetividad, los exámenes, ni la suerte (indicadores extrínsecos). Lo que indica que reconocen que su éxito se encuentra en función de motivadores intrínsecos y no externos.
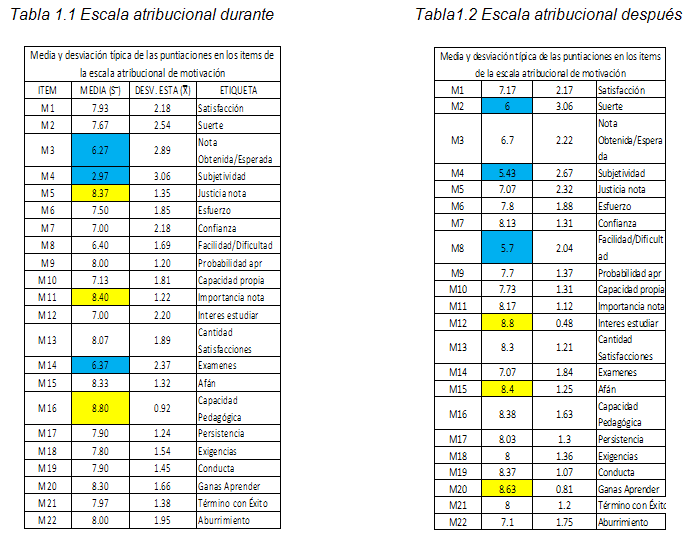
Complementariamente, el análisis de las tablas 1.3 y 1.4 ratifican las atribuciones de los alumnos sometidos a la estrategia de la Matemática en Contexto, observándose que existió un vire de una visión extrínseca a una intrínseca, toda vez que durante la implementación de la didáctica de la Matemática en Contexto, los valores de las medias de los ítem por categoría más altas pasó de la capacidad pedagógica del profesor a la de interés por aprender.
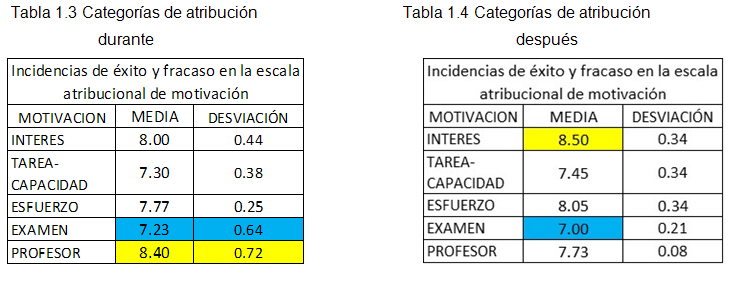
Los resultados muestran que la Escala Atribucional de Motivación de Logro (EAML) es confiable para identificar las atribuciones causales sobre el rendimiento en alumnos que fueron sometidos a la didáctica de la Matemática en Contexto.
En general los instrumentos de medición utilizados en esta investigación muestran un panorama global de las condiciones de motivación experimentadas por 29 alumnos antes, durante y después de implementada la didáctica de la Matemática en Contexto, observándose un cambio significativo de una motivación general extrínseca hacia una motivación general intrínseca. Así como de una diferencia significativa entre el rendimiento académico de los 29 alumnos que trabajaron con la didáctica de la Matemática en Contexto con respecto al grupo que no trabajó con ella.
La mayoría de los alumnos sintieron satisfacción cuando pudieron resolver eventos contextualizados, pero más satisfacción presentaron cuando defendieron su proyecto de investigación en el “1° Concurso aplicación de las ecuaciones diferenciales con herramientas computacionales”, porque se modificó y despertó en ellos un cambio de actitud y aptitud que los llevó a un proceso de confianza, satisfacción y participación tal que les permitió llegar más allá de los que se les pidió. Específicamente presentaron los programas de resolución de los eventos contextualizados tanto en el software de la calculadora TI-Nspire como en el software de MatLab vinculando la asignatura de Taller de herramientas computacionales con Ecuaciones diferenciales por un lado, y por otro lado demostrando un dominio y aplicación del software de Matlab para predecir los datos experimentales esperados. Cabe aclarar que el soporte del software de MatLab no se les enseñó, pero por su cuenta 3 de los 6 equipos presentaron los proyectos con dicho software, crearon un ambiente de competitividad y eficiencia, vinculando la matemática con diferentes áreas de contexto.
Conclusiones
Es importante conocer las causas a las que generalmente los estudiantes atribuyen sus resultados académicos; por ello, con base en los resultados obtenidos en la escala de atribuciones de la motivación al logro, después de implementada la estrategia didáctica de la Matemática en Contexto, se estableció que las atribuciones realizadas por los alumnos con el deseo de alcanzar el éxito y evitar el fracaso, fueron representadas por causas como la capacidad, el esfuerzo, y el interés, y en menor medida por el grado de dificultad de la tarea y la suerte, aunque se reconoce que puedan existir otras. La semblanza anterior indica un alto nivel atribucional hacia la motivación intrínseca, resultados que Weiner propone como ideales en estudiantes con altos niveles de motivación al logro.
Bibliografía
Camarena, P. G., (2001). Reporte del proyecto de investigación titulado: La matemática en el contexto de las ciencias, la resolución de problemas. ESIME-IPN.
Carrasco, C. (1993). Motivaciones sociales y desempeño. Material elaborado para el seminario cultura organizacional, calidad total y desempeño. Departamento de Investigación y Postgrado. UNEXPO, Barquisimeto.
De Faria, E. 2000. "La tecnología como herramienta de apoyo a la generación de conocimiento". Revista Innovaciones Educativas. San José: Editorial EUNED, año VII, número 12, 79-85.
Gómez, P. 1997. "Tecnología y Educación Matemática". Página Web http://www.uniandes.edu.co
Good, T. y Brophy, J. (1996). Psicología educative contemporánea. (5ta. ed.). Mexico. McGraw Hill.
Martínez C. 1996. "Explorando transformaciones de funciones con una calculadora gráfica". Memoria Décima Reunión Centroamericana y Caribe sobre Formación de Profesores e Investigación en Matemática Educativa. Puerto Rico.
National Council of Teachers of Mathematics Professional Standards for Teaching Mathematics, , Octubre 1996.
Ramirez B., K. Wayland 1996. "La calculadora TI-92 y su impacto en la enseñanza de ciencias y matemáticas". Memoria Décima Reunión Centroamericana y Caribe sobre Formación de Profesores e Investigación en Matemática Educativa. Puerto Rico.
Anexo 1
Escala Atribucional de Motivación de Logro
Propósito. Estimado estudiante, el propósito de esta encuesta, es recopilar tu opinión acerca de las atribuciones que otorgas a las Ecuaciones Diferenciales Aplicadas [EDA] en tu proceso de aprendizaje.
INICIO. Proporciona los datos que a continuación se te piden
Nombre _______________________________________________________________ Carrera ____________________ Semestre________________Edad ______________ Sex: F o M _________ |
INSTRUCCIONES
Por favor contesta las siguientes preguntas escogiendo el número que más refleja tu respuesta SI NO HAS ENTENDIDO BIEN LO QUE HAY QUE HACER, PREGUNTA A TU APLICADOR.
1. Valora el grado de satisfacción que tienes en relación con la nota de [EDA] de la evaluación pasada:
TOTALMENTTE SATISFECHO 9 8 7 6 5 4 3 2 1 NADA SATISFECHO
2. Valora la influencia de la suerte en tu nota de [EDA]:
INFLUYE MUCHO 1 2 3 4 5 6 7 8 9 NO INFLUYE NADA
3. Valora la relación existe entre la nota que obtuviste y la nota que esperabas obtener en [EDA]:
MEJOR DE LO QUE ESPERABAS 9 8 7 6 5 4 3 2 1 PEOR DE LO QUE ESPERABAS
4. Valora el grado de subjetividad en la calificación de evaluación del profesor de [EDA]:
TOTALMENTE SUBJETIVO 1 2 3 4 5 6 7 8 9 NADA SUBJETIVO
5. Valora la justicia de la nota de [EDA] en relación a tus merecimientos:
TOTALMENTE JUSTAS: 9 8 7 6 5 4 3 2 1 TOTALMENTE INJUSTAS
6. Valora el esfuerzo que tú haces actualmente para sacar buena nota en [EDA]:
NINGUN ESFUERZO 1 2 3 4 5 6 7 8 9 MUCHO ESFUERZO
7. Valora la confianza que tienes de sacar buena nota en [EDA]:
MUCHA CONFIANZA 9 8 7 6 5 4 3 2 1 NINGUNA CONFIANZA
8. Valora la facilidad/dificultad de las tareas escolares que realizas en [EDA]:
MUY DIFICIL 1 2 3 4 5 6 7 8 9 MUY FÁCIL
9. Valora la probabilidad de aprobar las [EDA] que crees que tiene este curso
MUCHA PROBABILIDAD 9 8 7 6 5 4 3 2 1 NINGUNA PROBABILIDAD
10. Valora tu propia capacidad para estudiar [EDA]:
MUY MALA 1 2 3 4 5 6 7 8 9 MUY BUENA
11. Valora la importancia que das a las buenas notas de [EDA]:
MUY IMPORTANTES PARA MI 9 8 7 6 5 4 3 2 1 NADA IMPORTANTES PARA MI
12. Valora el interés que te tomas por estudiar [EDA]:
NINGUN INTERES 1 2 3 4 5 6 7 8 9 MUCHO INTERES
13. Valora la cantidad de satisfacciones que te proporciona estudiar [EDA]:
MUCHAS SATISFACCIONES 9 8 7 6 5 4 3 2 1 NINGUNA SATISAFACIION
14. Valora el grado en que los exámenes influyen en aumentar o disminuir la nota que merecías en [EDA]:
DISMINUYE EN MI NOTA1 2 3 4 5 6 7 8 9 AUNMENTA MI NOTA
15. Valora el afán que tú tienes de sacar buenas notas en [EDA]:
MUCHO AFÁN 9 8 7 6 5 4 3 2 1 NINGÚN AFÁN
16. Valora la capacidad pedagógica de tu profesor de [EDA]:
MAL PROFESOR 1 2 3 4 5 6 7 8 9 BUEN PROFESOR
17. Valora tu persistencia después que no has conseguido hacer una tarea de [EDA] o esta te ha salido mal:
SIGO ESFORZANDOME AL MAXIMO 9 8 7 6 5 4 3 2 1 ABANDONO LAS TAREAS
18. Valora las exigencias que te impones a ti mismo respecto al estudio de [EDA]:
EXIGENCIAS MUY BAJAS 1 2 3 4 5 6 7 8 9 EXIGENCIAS MUY ALTAS.
19. Valora tu conducta cuando haces un problema difícil de [EDA]:
SIGO TRABAJNDO HASTA EL FINAL 9 8 7 6 5 4 3 2 1 ABANDONO RAPIDAMENTE
20. Valora tus ganas de aprender [EDA]:
NINGUNA GANA 1 2 3 4 5 6 7 8 9 MUCHÍSIMAS GANAS
21Valora la frecuencia de terminar con éxito una tarea de [EDA] que has empezado:
SIEMPRE TEMINO CON ÉXITO 9 8 7 6 5 4 3 2 1 NUNCA TERMINO CON ÉXITO
22. Valora tu aburrimiento n las clases de [EDA]:
SIMEPRE ME ABURRO 1 2 3 4 5 6 7 8 9 NUNCA ME ABURRO