

Resumen
En el marco educativo de la Licenciatura en Educación Secundaria con Especialidad en Matemáticas de la Escuela Normal de Naucalpan, la formación docente en el ámbito de la probabilidad y de la estadística exige proporcionar elementos que orienten la práctica de los futuros maestros en este contenido matemático en particular al interior del aula de la escuela secundaria. En este avance presentamos los resultados de la aplicación de un cuestionario dirigido a identificar las dificultades de comprensión de ideas fundamentales de estocásticos de futuros maestros de matemáticas de secundaria, en la antesala al inicio de sus prácticas de campo, correspondientes a su último año de la licenciatura para la docencia en la educación secundaria, lo anterior con la posibilidad de fortalecer las competencias docentes referentes a la enseñanza de estocásticos.
Palabras clave: Educación secundaria, estocásticos, docencia.
Introducción
El estudio al que se alude, de carácter cualitativo (Eisner, 1998), forma parte de un proyecto de investigación acerca del desarrollo de competencias para la enseñanza de las matemáticas y el dominio del contenido matemático correspondiente a estocásticos (probabilidad y estadística) entre estudiantes del último grado de la Escuela Normal de Naucalpan y su estrecha relación con su práctica docente. El objetivo es fortalecer las competencias que requieren los docentes en formación de la Licenciatura en Educación Secundaria con Especialidad en Matemáticas, en particular las referidas al dominio del conocimiento pedagógico relacionado con la enseñanza de estocásticos. La investigación se orienta, epistemológicamente, hacia las ideas fundamentales de estocásticos (Heitele, 1975); cognitivamente, hacia el rol de la intuición en las ideas de estocásticos Fischbein (1975); y socialmente, se considera la constitución del conocimiento derivado de las relaciones de los individuos con su entorno. (Steinbring, 1991). El dominio del contenido matemático corresponde a la predicción y el azar, así como tratamiento y presentación de la información en el plan de estudios de educación secundaria con especialidad en matemáticas 1999.
Este avance presenta los resultados de la aplicación de un cuestionario dirigido a identificar las dificultades de comprensión de ideas fundamentales de estocásticos de futuros maestros de matemáticas de secundaria, en la antesala al inicio de sus prácticas de campo, correspondientes a su último año de la licenciatura para la docencia en la educación secundaria.
Si bien el instrumento utilizado permite una aproximación de carácter descriptivo a la información conseguida, señalase que interesó el procedimiento realizado por el estudiante , de tal modo que el tipo de justificación otorgada y el tipo de errores identificados fueron aspectos cualitativos que se consideraron para analizar el tipo de respuesta y justificación al cuestionario.
Si bien es cierto que actualmente la probabilidad es un área de la matemática que cobra cada día más importancia en relación con las otras áreas del conocimiento humano, las prioridades de los programas de estudio para la educación secundaria (SEP, 2011) parece no incluir temas como el referente a los usos sociales de procesos de azar, estimación de probabilidades mediante las frecuencias relativas, es decir, está ausente la frecuencia relativa.
Problematización
En nuestro país existen un plan y programa de estudio nacional que prescribe las materias, contenidos y enfoque pedagógico que orienta la acción educativa en la educación básica (preescolar, primaria y secundaria). En particular el de matemáticas proporciona información sobre los propósitos, el enfoque y los alcances en cuanto a la formación matemática de los estudiantes, en este caso de educación básica en general y la educación secundaria en particular.
Dado que, el escenario que se vislumbra es, que la probabilidad, el azar y los fenómenos estocásticos siguen siendo un tema secundario, reducido al manejo de datos y presentación de información en los planes y programas de educación secundaria mexicano, carece de la profundidad en el tratamiento de los procesos cognitivos y de pensamiento crítico necesario para comprender la continuidad y el razonamiento lógico que fundamenta los eventos aleatorios en la vida cotidiana de los estudiantes de secundaria y no incluye temas como el referente a los usos sociales de procesos de azar, estimación de probabilidades mediante las frecuencias relativas, es decir, está ausente la frecuencia relativa. La enseñanza de la probabilidad se orienta en el uso de expresiones algebraicas para determinar su cálculo, dejando de lado el desarrollo de la intuición probabilística.
Algunas investigaciones desarrolladas en México, proporcionan evidencias de la poca importancia y escasa trascendencia que se le otorga en los distintos niveles de educación básica a la enseñanza de estocásticos en general y de la probabilidad en particular (Galván, 1996; Alquicira, 1998; Perrusquía, 1998; Elizarraras, 2004; Vázquez, 2004, López, 2006). Esta situación propicia una adquisición parcial de conocimientos, que en conjunto conducen a que los estudiantes exhiban un razonamiento limitado de temas sobre probabilidad en el nivel medio superior y superior (de León, 2002).
En relación con el tema de probabilidad, surge entonces la pregunta: ¿Qué elementos requiere el docente en formación para posibilitar la enseñanza de estocásticos en el aula de secundaria?
Método
Se plantearon 10 problemas, de tal manera que los estudiantes pudieran justificar su respuesta. La Tabla 1 muestra la caracterización del instrumento.
Tabla 1. Ideas fundamentales implícitas en los problemas propuestas.
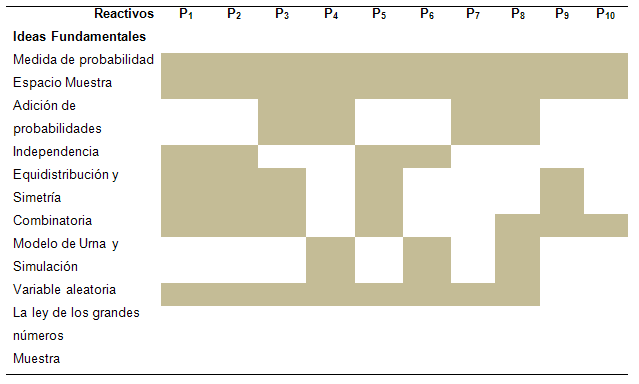
El tipo de reactivos corresponde al nivel Secundaria, para cuya docencia se preparaban los participantes en esta investigación.
A cada respuesta se aplicó la célula de análisis (Ojeda, 2006); se consideró el tipo de justificación proporcionada respecto a las ideas fundamentales de estocásticos, a los otros conceptos matemáticos, requeridos para justificar la respuesta, a los recursos semióticos utilizados en la justificación y a los términos referentes a estocásticos empleados en la respuesta.
Uno de los propósitos del instrumento fue obtener información del conocimiento de estocásticos adquirido de los estudiantes de la Licenciatura en Educación con Especialidad en Matemáticas al término del sexto semestre.
Si bien el instrumento nos permitió una aproximación de carácter descriptivo a la información obtenida, nos interesó en particular el procedimiento realizado por el docente en formación, de tal modo que el tipo de justificación otorgada y el tipo de errores identificados, fueron aspectos cualitativos que se consideraron para analizar el tipo de respuestas y justificación del estudiante normalista.
Todos los problemas expuestos, responden al enfoque clásico de la probabilidad Algunos de los problemas fueron planteados considerando el contenido del Libro para el Maestro (Alarcón et. el., 1999) y las lecciones 52, 54 y 55 del libro de texto (Filloy et. Al., 2001). Así, para el problema 7 se consideró la lección 52; para los problemas 2 y 9 la lección 54; para el problema 3, la lección 55; para los problemas 1,5,6 y 8, se consideró el Libro para el Maestro (págs.. 277,394,397 y 387 respectivamente). El problema 10 se elaboró considerando una situación cotidiana del estudiante. Todos los problemas se plantearon en lengua natural.
Resultados del análisis de las respuestas
La Tabla 2 resume la cantidad de respuestas correctas por problema.
Tabla 2. Cantidad de respuestas correctas en el instrumento.
P1 |
Correctas |
13 |
65% |
P2 |
Correctas |
10 |
50% |
P3 |
Correctas |
13 |
65% |
P4 |
Correctas |
18 |
90% |
P5 |
Correctas |
16 |
80% |
P6 |
Correctas |
17 |
85% |
P7 |
Correctas |
18 |
90% |
P8 |
Correctas |
8 |
40% |
P9 |
Correctas |
8 |
40% |
P10 |
Correctas |
0 |
100% |
P1 En dos volados consecutivos, ¿Cuál es la probabilidad de obtener sólo águilas?
La respuesta a este problema informa si el estudiante identifica para dos volados consecutivos el espacio muestra del fenómeno, la independencia de los ensayos y si aplica la regla del producto de probabilidades.
Respecto a este problema, siete estudiantes no advirtieron el espacio muestra del fenómeno para situaciones compuestas. Fischbein (1975, en Colín et. al., 1993) argumenta “el caso de eventos independientes, una intuición primaria facilita la comprensión de la ley de la multiplicación, pero el cálculo final no se puede encontrar intuitivamente” (pág.25).
P2 Iván, Néstor y Josías, van a sortear un libro de aventuras de la siguiente manera: Iván tira dos volados. Si en los dos volados sale águila, gana Iván. Si en los dos volados sale sol, gana Néstor, si sale águila y sol, gana Josías. ¿Tienen los tres la misma probabilidad de ganar el libro?; ¿Quién de los tres ganará el libro?
La respuesta a este problema informa si el estudiante identifica la independencia de los ensayos, el espacio muestra y combinatoria. Diez estudiantes no identificaron el espacio muestra, aplican de manera errónea la regla del producto.
P3 ¿Cuál es la probabilidad de que al lanzar dos dados, la suma de las caras hacia arriba sea 7?
Las ideas fundamentales que el estudiante debe identificar en este problema son: espacio muestra, combinatoria, regla de la suma, equidistribución y simetría, finalmente la variable aleatoria. Siete estudiantes no identificaron estas ideas fundamentales. De acuerdo con Fischbein (1975 en Colín et. Al., 1993, pág.35) “aún en las operaciones formales, las técnicas combinatorias no se adquieren espontáneamente; la enseñanza es necesaria”
P4 En un frasco oscuro hay 15 canicas idénticas (igual tamaño y forma), pero en distinto color: 10 canicas son rojas y 5 son blancas. Si se saca una canica sin mirar al interior del frasco ¿Cuál es la probabilidad de obtener una canica blanca?
Siendo las canicas iguales, las posibilidades de sacar cualquier canica son iguales. Las ideas fundamentales implícitas en este problema son: regla de la adición, espacio muestra, modelo de urna y variable aleatoria.
Dos estudiantes no distinguieron el espacio muestra, con el restante.
P5 Se arroja un dado (seis caras iguales) y una moneda. ¿Cuál es la probabilidad de obtener cinco en la “cara” del dado que quede hacia arriba y “sol” en la cara de la moneda?
Cuatro estudiantes no establecieron el espacio muestra del fenómeno en cuestión y, por consiguiente, no hay evidencia de que hayan emitido un razonamiento probabilístico para aplicar la regla del producto de probabilidades. A este respecto Heitele (1975, pág. 4) subraya que el concepto de independencia resulta difícil aún para los matemáticos que tienen conocimiento de este concepto.
P6 Una caja contiene 5 canicas blancas y 5 canicas rojas, sin ver sacamos una canica y la dejamos fuera, luego sacamos otra canica ¿Cuál es la probabilidad de sacar primero una canica blanca y después roja?
La puesta en juego de este problema, permitió identificar que sólo tres estudiantes tuvieron dificultades para identificar las condiciones del problema.
P7 Se lanza un dado (seis caras) ¿Cuál es la probabilidad de obtener puntos que serán un número par?
Con este problema se exploran las ideas de espacio muestra, la regla de la adición, medida de probabilidad, equidistribución y simetría. Aquí sólo dos estudiantes tuvieron dificultad con estas ideas.
P8 Se tienen tres canicas rojas idénticas y una canica blanca en una bolsa ¿Cuál es la probabilidad de que al sacar al mismo tiempo tres canicas, las tres sean rojas?
Doce estudiantes no identificaron los casos posibles, de los cuales sólo uno corresponde al evento que interesa; por lo que se tuvo dificultad con las siguientes ideas fundamentales: espacio muestra, variable aleatoria, modelo de urna y simulación.
P9 Un examen de Física consta de dos partes: una parte de laboratorio, donde debes saber un experimento que te propongan. Una parte oral, donde debes responder preguntas sobre teoría. El programa consta de diez experimentos, numerados del 1 al 10 y seis temas para la parte teórica señalados con letras A, B, C. D. E y F. Para aprobar el examen, debes saber ambas cosas: el experimento y el tema que te toquen. Como no has estudiado bien para tú examen, de los 10 experimentos sólo te sabes del 1 al 6; y de los 6 temas para el examen oral, sólo los 4 primeros (el A, el B, el C y el D) ¡piensa bien antes de contestar tu respuesta!
a) ¿Qué es más probable, que apruebes el examen o que repruebes el examen?
b) te sabes 4 temas del examen oral ¿Cuántos experimentos necesitas saber como mínimo para tener mayor probabilidad de aprobar que de reprobar?
Las ideas fundamentales implícitas en este problema son: espacio muestra y combinatoria, doce de los estudiantes tuvieron dificultades de comprensión de estas ideas.
P10 Al terminar un partido de fútbol entre Toluca (local) y el América (visitante), Toluca anotó 3 goles y el América anotó 2 goles. ¿Cuál es la probabilidad que existe de que el equipo de Toluca haya perdido al término del primer tiempo?
En este problema los veinte estudiantes no contestaron correctamente.
Las dificultades que enfrentan los estudiantes permiten indicar el conocimiento o el desconocimiento de las ideas fundamentales de estocásticos, cuya repercusión puede propiciar o no la comprensión de tales ideas durante su práctica educativa con los estudiantes de educación secundaria.
Comentarios generales
Dado que en la formación matemática de los estudiantes de nivel medio superior el tratamiento de la probabilidad es hasta sexto semestre, con frecuencia se le asigna poca importancia o bien, en el mejor de los casos se trata en forma breve, si en algunas ocasiones no se introducen actividades donde se utilicen recursos concretos (dados, monedas, ruletas, etc.) para la enseñanza de este tema. Esta formación se refleja en la manera en que estudiantes normalistas afrontan la resolución de problemas que implican competencias sobre estocásticos.
Por tanto, es importante la introducción de actividades de enseñanza en el aula de fenómenos aleatorios mediante la utilización física de estos recursos o bien empleando programas de cómputo; pues proporcionan a los estudiantes experiencias empíricas sobre experimentos aleatorios que le permitan evaluar naturalmente la probabilidad, así como también, sienta las bases para un buen desarrollo del pensamiento probabilístico. Son evidentes las deficiencias que siguen presentando los estudiantes de la Licenciatura en Educación con Especialidad en Matemáticas en la comprensión de la probabilidad.
Referencias Bibliográficas
Alarcón Bortolussi, Jesús Et. al. (1994). Libro para el maestro. Educación secundaria. Matemáticas. Subsecretaria de Educación Básica y Normal. Dirección General de Materiales y Métodos educativos. México. SEP.
Alquicira, Ma. I.:1998, Probabilidad: Docencia y Praxis. Hacia una fundamentación Epistemológica para la Educación Secundaria. Tesis de Maestría. DME, Cinvestav del IPN. México.
Colín, J. Garnica,I., Ojeda, A. (1993) Intuición y Probabilidad desde el punto de vista de Fischbein. Cuadernos de investigación No 26 Año VII. Programa Nacional de Formación y Actualización de Profesores de Matemáticas. Cinvestav del IPN. México
Eisner, Elliot W.: 1998, El ojo ilustrado. Indagación cualitativa y mejora de la práctica educativa. Paidós. España.
Elizarraras, Saúl: 2004, Enseñanza y comprensión del enfoque frecuencial de la probabilidad en segundo grado de secundaria, tesis de Maestría, DME, Cinvestav-IPN, México.
Filloy Yagüe, E. et. al. (2001). Matemática educativa. Primer grado, McGraw Hill, México.
Fischbein,E. (1975) The Intuitive Sources of probabilistic Thinking in Children. D. Reidel Publishing Company, USA.
Galván, M.: 1996, Nubes y relojes, Tesis de maestría.DME, Cinvestav del IPN. México.
Heitele, D.: 1975. An Epistemological View on Fundamental Stochastic Ideas. Educational Studies of Mathematics 6. págs. 187-205, Reidel. Holland.(Traducción para fines educativos, Ojeda, A. M.; Departamento de Matemática Educativa del Cinvestav-IPN, 1993, México).
León, de José: 2002. Comprensión de la ley de los grandes números de estudiantes de ciencias sociales. Tesis de doctorado. DME, Cinvestav del IPN. México.
López Molina, J.M.: 2006. Comprensión de la ley de los grandes números en el tercer grado de secundaria. Tesis de Maestría. DME, Cinvestav del IPN. México.
Ojeda, A. M. (2006). Estrategia para un perfil nuevo de docencia: un ensayo en la enseñanza de estocásticos. En Filloy (Ed) Matemática Educativa, treinta años (pp. 257-281). México: Santillana-Cinvestav.
Perrusquia, E.:1998, Probabilidad y aritmética: Un estudio epistemológico en el estadio medio. Dificultades de interpretación. Tesis de Maestría. DME, Cinvestav del IPN, México.
SEP, 2011: Plan y programas de Estudio. Educación básica. Secundaria. Subsecretaria de Educación Básica y normal. Dirección General de Materiales y Métodos Educativos, México.
Steinbring, H.:1991, The concept of Chance in Everyday Teaching: Aspects of social Epistemology of Mathematical Knowledge. Educational Studies of Mathematics 22: 503-522. Kluwer Academic Publishers. Holland.
Vázquez Pérez, Orlando: 2004, Enseñanza y comprensión del enfoque clásico de la probabilidad de estudiantes de primer grado de secundaria. Tesis de Maestría. DME, Cinvestav del IPN. México.